How To: The Simple No-Prop Method for Fixing a Wobbly Table Super Fast

As sure as death and taxes, sitting at a wobbly table at one time or another is inescapable. With your weight on it, the table shifts from one end to the other, lifting one leg in the air and then the other; a parade of seesaws, especially if you have someone sitting on the other end.

Inevitably, someone will fold a piece of paper and slide it under the raised table leg, but that doesn't always bode well, as the pressure from the table and its occupants will crush the paper until it loses its ability to stabilize the leg completely. Sometimes a coaster will work well, but then that's one less coaster for your beer.

Well, turns out that fixing an off-balanced table is much easier than you thought...

Just Rotate the Damn Table

Matthias Kreck, a professor at the the University of Bonn in Germany, explains in the video below that anyone can balance a table simply by shifting it 45-degrees in a circle, given that the table is square and indeed has even legs.

According to Kreck, somewhere in that 45-degree shift there will be a moment of stability where all of the table legs will be at ground level. It's not the table that's uneven—it's the ground. And what does he have to prove his theory?

Math!

Surprisingly, the mathematics for this theory dates back to the late 1960s, where Roger Fenn, a PhD student at the University of London, couldn't get a table to stop wobbling. So, of course, Fenn then decided to write a proof that showed how to stabilize the table. Unfortunately, while he did get the answer, he couldn't come up with why.

Thirty years later, both Burkard Polster (a mathematician) and Andr Martin (a physicist) detailed the proof that Fenn was trying to find, so now we have the mathematics to back up what Kreck says about balancing out a table.

How exactly does this math work?

How the Math Works

Say we have a square off-kilter table on the ground, with one leg sticking up in the air. We'll call this leg, LEG 1.

The rest of the legs, which will be fixed to the ground in this experiment, will be designated with LEG 2, LEG 3, and LEG 4, like in the drawing below.

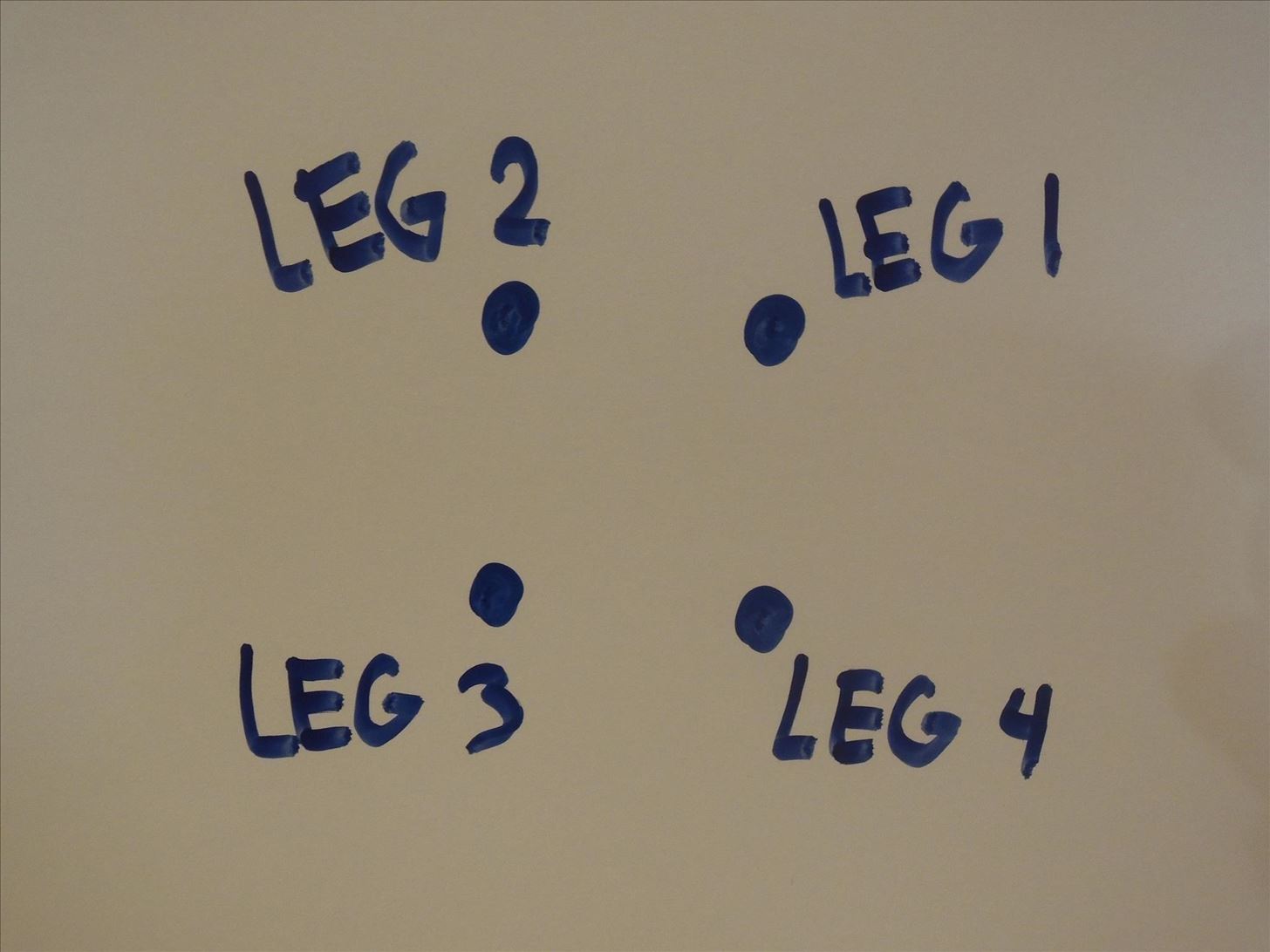
Now we measure the height (x) between the floor and LEG 1, which we will take in measurements of time (t). Before we begin moving the table, we have the following.

t=0, x>0

Now let's shift the table. When the table is being moved, we want the position of LEG 1 to lie above the position where LEG 2 initially was, moving LEG 2 where LEG 3 was, and so on.

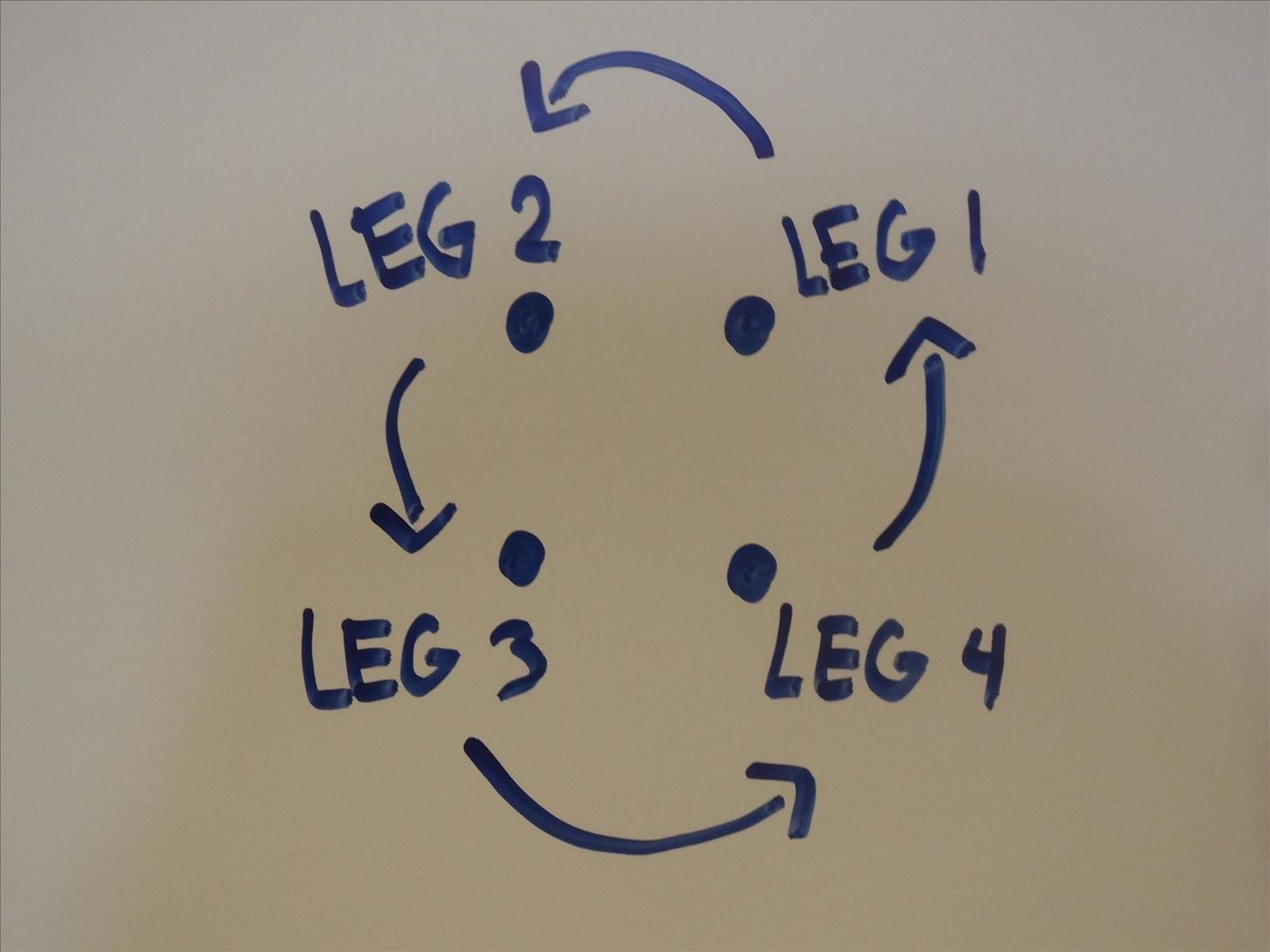
During the movement of LEG 1 to the previous position of LEG 2, we're making measurements of the height (in time), which gives us the following function.

f(t)

Now here's the fun part.

Remember that LEGS 2, 3, and 4 are always at ground level? If LEG 1 is moved to the position of LEG 2, it will then be below the ground since the other legs are fixed, leaving it with a negative or less than zero height during this time (which we'll call 1).

t=1, x<0

If you don't quite get why LEG 1 now has a negative height, let me explain it another way. The only reason that LEG 1 is initially above ground level is because its opposite leg (in this case, LEG 3) must be below ground level, due to the irregular ground.

Now lets draw out both of the equations into a graph, to better understand it. Starting from the initial height (positive) at time zero, we draw a curved line (since we don't know how irregular the ground is) and connect it to the final height (negative) at time one.

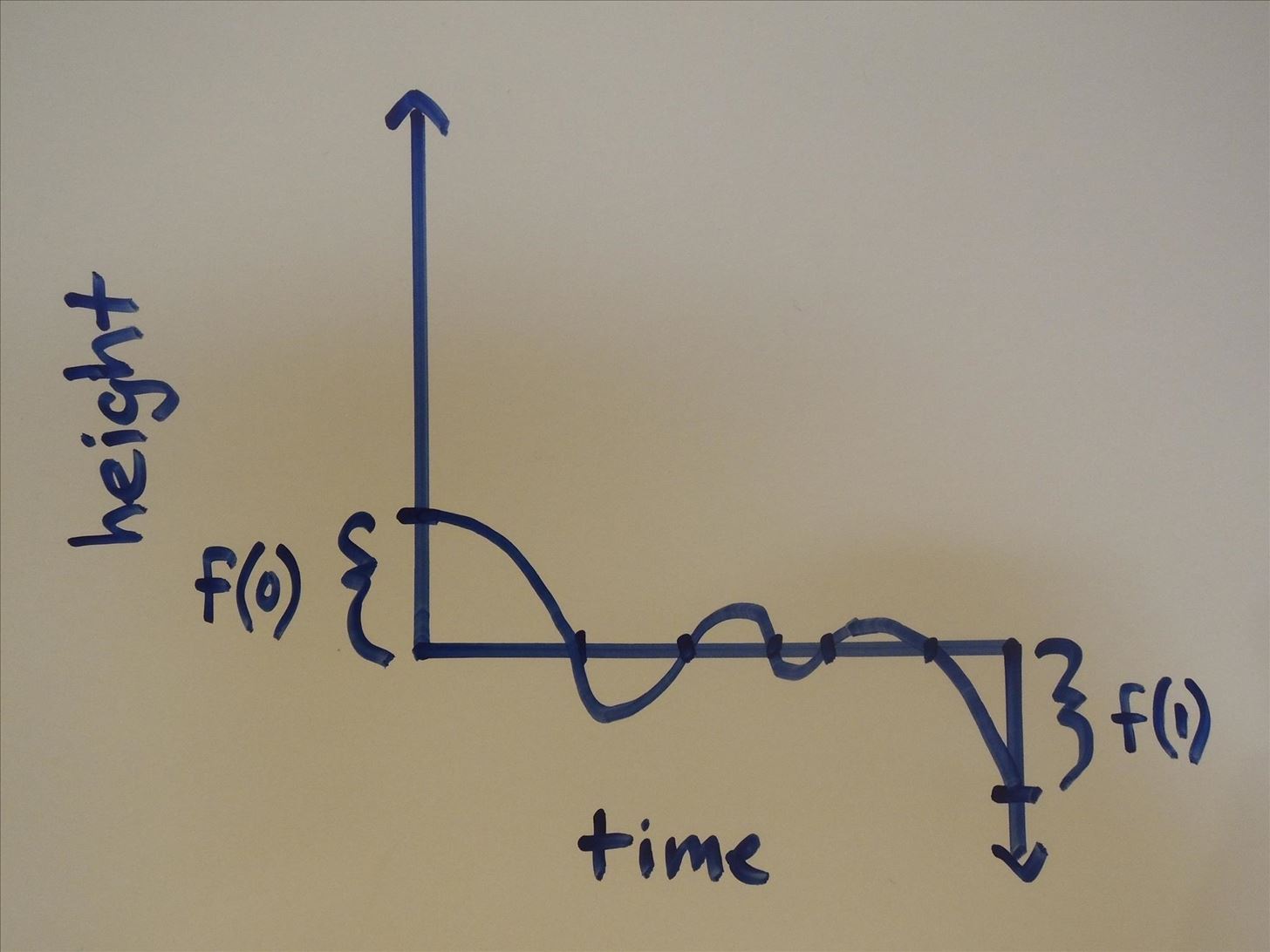
And here is where we notice that we have to cross the plane where x=0, so in theory, LEG 1 has to at one point be at ground level (x=0). According to the Intermediate value theorem, if you have a continuous function with an interval, then it must take any value in-between as well, which in this case is zero because it starts off positive and ends up negative.

As for how many values of zero the graph has all depends on how irregular the ground is. There might be only one value of zero, or several. But there has to be at least one.

And that's where your table can safely rest, on all fours, without wobbling side to side, thanks to math.

Do You Really Need to Use Math, Though?

No. Instead of using wads of paper, coasters, or complicated math problems, just rotate the table. Eventually, somewhere in-between a full quarter turn (90 degrees), you'll get to a point where it'll wobble no more. Simple as that.